Non Linear Optimizers
🚀 Using Different Non-Linear Optimizers
Below are implementations of this approach using four popular non-linear optimizers:
- Ceres Solver (C++) , https://github.com/ceres-solver/ceres-solver
- NLopt (C++) , https://github.com/stevengj/nlopt
- COBYLA (Python).
Non-linear optimizers are essential in SLAM and robotics for solving complex problems involving localization, mapping, and sensor calibration. They help:
1- Refine Robot Poses: Correct errors in the robot’s position and orientation to build accurate maps.
2- Sensor Fusion: Align data from multiple sensors (e.g., cameras, LiDAR) by minimizing discrepancies.
3- Loop Closure: Fix accumulated errors when revisiting previous locations.
4- Inverse Kinematics: Calculate joint angles for robotic arms.
5- Path Planning: Optimize paths to avoid obstacles and minimize energy or time.
Popular optimizers include Ceres Solver, GTSAM, and g2o. They handle non-linear relationships efficiently, ensuring accuracy and robustness in real-world robotics tasks.
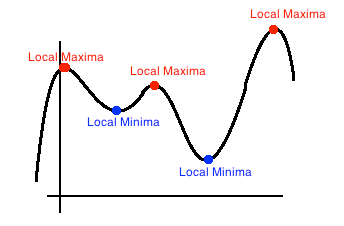
🔎 Explanation of the Code
Objective Function:
The goal is to minimize the negative of arr[i] to effectively maximize arr[i].
Index Bounds:
Constraints ensure the index stays within the valid range of the array.
Initial Guess:
We start the optimization from the middle of the array.
📊 Complexity Analysis
Time Complexity:
Approximately O(log n) or higher due to the iterative nature of non-linear optimizers.
Space Complexity:
O(1) – Minimal additional memory usage.
🛠️ 1. Ceres Solver (C++ Implementation)
#include "ceres/ceres.h"
#include "glog/logging.h"
#include <vector>
#include <iostream>
#include <cmath>
// Cost function for finding a peak
class PeakCostFunction : public ceres::SizedCostFunction<1, 1> {
public:
PeakCostFunction(const std::vector<double>& arr) : arr_(arr) {}
virtual bool Evaluate(double const* const* parameters, double* residuals, double** jacobians) const {
double index = parameters[0][0];
int rounded_index = static_cast<int>(std::round(index));
// Clamp index within valid bounds
rounded_index = std::max(0, std::min(rounded_index, static_cast<int>(arr_.size()) - 1));
residuals[0] = -arr_[rounded_index];
// Optional Jacobian computation
if (jacobians && jacobians[0]) {
jacobians[0][0] = 0.0;
}
return true;
}
private:
const std::vector<double>& arr_;
};
int main(int argc, char** argv) {
google::InitGoogleLogging(argv[0]);
std::vector<double> arr = {1.0, 3.0, 20.0, 4.0, 1.0};
double index = 2.0;
ceres::Problem problem;
problem.AddResidualBlock(new PeakCostFunction(arr), nullptr, &index);
problem.SetParameterLowerBound(&index, 0, 0.0);
problem.SetParameterUpperBound(&index, 0, arr.size() - 1);
ceres::Solver::Options options;
options.minimizer_progress_to_stdout = true;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
int peak_index = static_cast<int>(std::round(index));
std::cout << "Peak found at index: " << peak_index << ", Value: " << arr[peak_index] << "\n";
return 0;
}
🛠️ 2. NLopt (C++ Implementation)
#include <nlopt.hpp>
#include <iostream>
#include <vector>
#include <cmath>
// Objective function: negative of the array value
double objective_function(const std::vector<double>& x, std::vector<double>& grad, void* data) {
std::vector<double>* arr = static_cast<std::vector<double>*>(data);
int index = static_cast<int>(std::round(x[0]));
index = std::max(0, std::min(index, static_cast<int>(arr->size()) - 1));
return -(*arr)[index];
}
int main() {
std::vector<double> arr = {1.0, 3.0, 20.0, 4.0, 1.0};
double initial_guess = 2.0;
nlopt::opt optimizer(nlopt::LN_BOBYQA, 1);
optimizer.set_lower_bounds({0.0});
optimizer.set_upper_bounds({static_cast<double>(arr.size() - 1)});
optimizer.set_min_objective(objective_function, &arr);
optimizer.set_xtol_rel(1e-4);
try {
double result_index = initial_guess;
double min_value;
optimizer.optimize({result_index}, min_value);
int peak_index = static_cast<int>(std::round(result_index));
std::cout << "Peak found at index: " << peak_index << ", Value: " << arr[peak_index] << "\n";
} catch (std::exception& e) {
std::cerr << "NLopt failed: " << e.what() << "\n";
}
return 0;
}
🛠️ 3. COBYLA (Python Implementation)
import numpy as np
from scipy.optimize import minimize
def objective(x, arr):
idx = int(round(x[0]))
idx = max(0, min(len(arr) - 1, idx))
return -arr[idx]
def constraint_lower(x):
return x[0]
def constraint_upper(x, n):
return n - 1 - x[0]
def find_peak(arr):
initial_guess = [len(arr) / 2]
constraints = [
{'type': 'ineq', 'fun': constraint_lower},
{'type': 'ineq', 'fun': lambda x: constraint_upper(x, len(arr))}
]
result = minimize(objective, initial_guess, args=(arr,), constraints=constraints, method='COBYLA')
peak_index = int(round(result.x[0]))
return peak_index, arr[peak_index]
# Example usage
arr = [1, 3, 20, 4, 1, 0]
peak_index, peak_value = find_peak(arr)
print(f"Peak found at index: {peak_index}, Value: {peak_value}")
🛠️ 4. GTSAM (C++ Implementation)
#include <gtsam/nonlinear/NonlinearFactorGraph.h>
#include <gtsam/nonlinear/Values.h>
#include <gtsam/nonlinear/GaussNewtonOptimizer.h>
#include <gtsam/nonlinear/NonlinearEquality.h>
#include <gtsam/inference/Symbol.h>
#include <iostream>
#include <vector>
#include <cmath>
using namespace gtsam;
using namespace std;
// Cost function for finding the peak
class PeakFactor : public NoiseModelFactor1<double> {
public:
PeakFactor(Key key, const vector<double>& arr)
: NoiseModelFactor1(noiseModel::Isotropic::Sigma(1, 1.0), key), arr_(arr) {}
// Evaluate the error for the given value
Vector evaluateError(const double& index, boost::optional<Matrix&> H = boost::none) const override {
int rounded_index = static_cast<int>(round(index));
rounded_index = max(0, min(rounded_index, static_cast<int>(arr_.size()) - 1));
if (H) {
(*H)(0, 0) = 0.0; // Jacobian: derivative is zero (since it's a discrete lookup)
}
// Return the negative of the array value (for maximizing the value)
return Vector1(-arr_[rounded_index]);
}
private:
const vector<double>& arr_;
};
int main() {
// Initialize the array with some values
vector<double> arr = {1.0, 3.0, 20.0, 4.0, 1.0};
// Initial guess for the peak index
double initial_index = 2.0;
// Create a NonlinearFactorGraph
NonlinearFactorGraph graph;
graph.add(boost::make_shared<PeakFactor>(Symbol('x', 0), arr));
// Initial values
Values initial;
initial.insert(Symbol('x', 0), initial_index);
// Optimize using Gauss-Newton
GaussNewtonParams params;
params.setVerbosity("ERROR");
GaussNewtonOptimizer optimizer(graph, initial, params);
Values result = optimizer.optimize();
// Retrieve the optimized peak index
double optimized_index = result.at<double>(Symbol('x', 0));
int peak_index = static_cast<int>(round(optimized_index));
cout << "Peak found at index: " << peak_index << ", Value: " << arr[peak_index] << endl;
return 0;
}
Some examples of Real world use cases of these algorithms
Bundle Adjustment:
Optimizes both the camera poses and 3D feature points to minimize reprojection error.
Bundle adjustment is computationally intensive and requires efficient non-linear solvers.
📌 Example: Visual SLAM Using GTSAM
NonlinearFactorGraph graph;
noiseModel::Isotropic::shared_ptr model = noiseModel::Isotropic::Sigma(6, 0.1);
// Add relative pose constraints
graph.emplace_shared<BetweenFactor<Pose3>>(Symbol('x', 0), Symbol('x', 1), relative_pose, model);
// Initial guesses
Values initial_estimates;
initial_estimates.insert(Symbol('x', 0), Pose3(Rot3(), Point3(0, 0, 0)));
initial_estimates.insert(Symbol('x', 1), Pose3(Rot3(), Point3(1, 0, 0)));
// Optimize the graph
GaussNewtonOptimizer optimizer(graph, initial_estimates);
Values result = optimizer.optimize();
Pose Graph Optimization:
Visual SLAM systems generate a graph where nodes represent camera poses and edges represent constraints (from odometry, feature matching, or loop closure).
Non-linear solvers minimize the error across this pose graph to refine the robot's trajectory and map.
Sensor Fusion:
Combining data from different sensors (e.g., IMU and camera) using non-linear optimization to improve localization accuracy.
Dynamic Systems with Non-Linear Dynamics:
When dealing with non-linear systems (e.g., self-driving cars, robotic manipulators), MPC relies on non-linear optimization solvers to find optimal control actions.
🚀 Typical Optimization Problem in MPC
Objective: Minimize the cost function:
$$ \min_{u_0, \dots, u_{N-1}} \sum_{k=0}^{N-1} \left( \|x_k - x_{\text{ref}}\|_Q^2 + \|u_k\|_R^2 \right) $$
Subject to the system dynamics:
$$ x_{k+1} = f(x_k, u_k) $$
Where:
- \( x_k \): System state at time step \( k \)
- \( u_k \): Control input at time step \( k \)
- \( x_{\text{ref}} \): Desired reference state
- \( Q \): Weight matrix for state penalties
- \( R \): Weight matrix for control penalties
- \( f(x_k, u_k) \): Non-linear system dynamics
import nlopt
import numpy as np
# System dynamics: x_next = x + u
def system_dynamics(x, u):
return x + u
# Objective function: minimize deviation from reference
def objective(u, grad, x, x_ref):
if grad.size > 0:
grad[0] = 2 * (x + u[0] - x_ref)
return (x + u[0] - x_ref) ** 2
# MPC setup
def mpc_controller(x, x_ref):
opt = nlopt.opt(nlopt.LN_COBYLA, 1)
opt.set_lower_bounds([-1.0])
opt.set_upper_bounds([1.0])
opt.set_min_objective(lambda u, grad: objective(u, grad, x, x_ref))
opt.set_xtol_rel(1e-4)
u_opt = opt.optimize([0.0])
return u_opt
# Example usage
x = 0.0
x_ref = 5.0
control = mpc_controller(x, x_ref)
print(f"Optimal control: {control}")
📊 Comparison of Non-Linear Solvers
| Solver | Language | Gradient Requirement | Constraints Support | Best For |
|---|---|---|---|---|
| Ceres Solver | C++ | Yes | Yes | Large-scale optimization, robotics, SLAM |
| NLopt | C/C++ | Optional | Yes | General non-linear optimization |
| COBYLA | Python (SciPy) | No | Yes | Derivative-free optimization with constraints |
| GTSAM | C++ | Yes | Yes | Factor graphs, SLAM, robotics |
| g2o | C++ | Yes | Limited | Graph-based optimization, SLAM |
✅ Pros and Cons of Non-Linear Solvers
| Aspect | Pros | Cons |
|---|---|---|
| Flexibility | Can handle complex, non-linear relationships. | May require problem-specific tuning. |
| Accuracy | Achieves high-precision solutions. | Sensitive to initial guesses (may get stuck in local minima). |
| Constraints | Supports various types of constraints. | Constraint handling can increase computation time. |
| Gradient Use | Efficient with gradient information (when available). | Requires gradient calculation or approximation (can be costly). |
| Applications | Widely used in SLAM, robotics, and control systems. | Not always suitable for real-time applications due to computation time. |